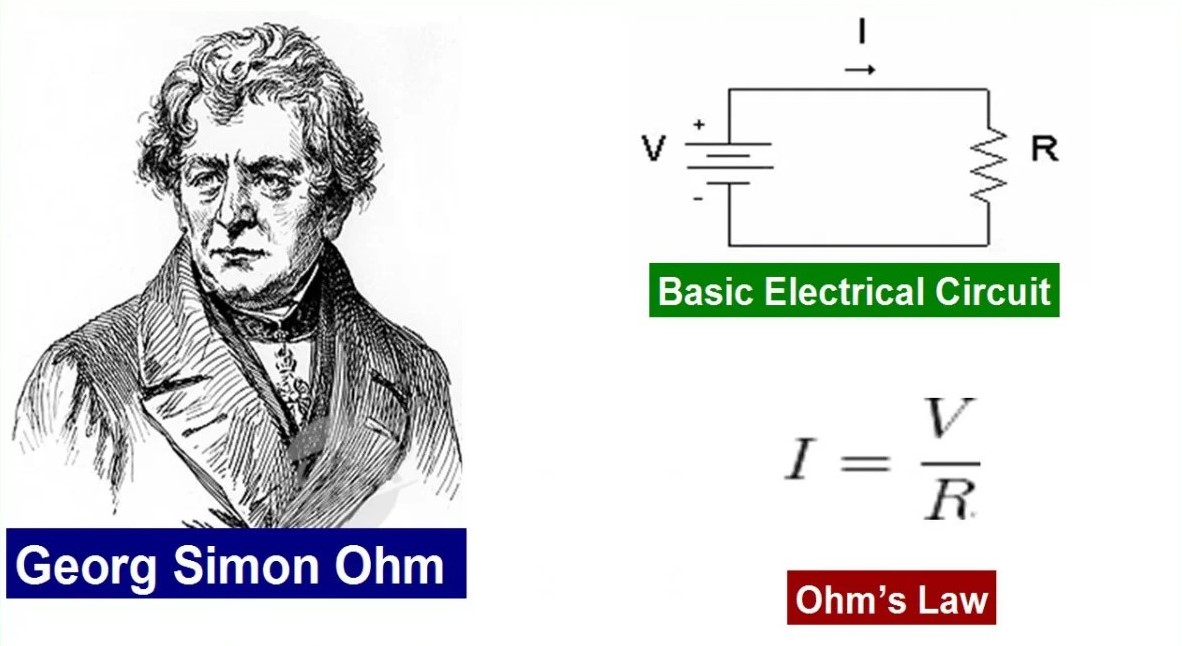
Ohm’s Law
Ohm’s Law is one of the fundamental principles in electrical engineering and plays a crucial role in circuit analysis. It establishes a relationship between the voltage across a resistor, the current flowing through it, and its resistance. According to Ohm’s Law, the current passing through a conductor is directly proportional to the voltage applied across it and inversely proportional to its resistance.
The mathematical equation for Ohm’s Law is expressed as follows:
V = I × R
Where:
V is the voltage in volts (V),
I is the current in amperes (A),
and R is the resistance in ohms (Ω).
This equation implies that as the voltage increases, the current flowing through the circuit also increases, assuming the resistance remains constant. Similarly, if the resistance increases while the voltage remains constant, the current decreases.
The significance of Ohm’s Law lies in its ability to help predict and control the behavior of electrical circuits. By applying this law, engineers and technicians can determine the appropriate values of voltage, current, and resistance required for satisfactory circuit operation. Ohm’s Law forms the foundation for many other circuit laws and theorems, making it an essential concept to understand in electrical engineering.
Additionally, Ohm’s Law can be used to calculate missing values. For instance, if we know the voltage across a resistor and its resistance, we can use Ohm’s Law to calculate the current flowing through it. Likewise, if we know the current and resistance, we can determine the voltage.
Understanding Ohm’s Law is crucial for circuit analysis, troubleshooting, and designing electrical systems. It provides us with valuable insights into the behavior of electrical components and their interaction within a circuit.
Kirchhoff’s Voltage Law (KVL)
Kirchhoff’s Voltage Law (KVL) is a fundamental principle in electrical circuit analysis. It states that the algebraic sum of the voltages in any closed loop in a circuit is equal to zero. This law is based on the principle of conservation of energy, which states that energy cannot be created or destroyed but is rather transferred or transformed.
KVL is useful in analyzing circuits with multiple voltage sources and resistors connected in series or parallel. It allows us to calculate unknown voltages or verify the accuracy of circuit calculations.
The application of Kirchhoff’s Voltage Law involves the following steps:
- Identify the closed loop or loops in the circuit.
- Assign polarities to the voltages based on the assumed direction of current flow.
- Apply KVL by summing up the voltages around each loop, taking into account the polarities.
- Set the sum of the voltages equal to zero, considering the signs and directions of the voltage drops and rises.
- Solve the resulting equations simultaneously to find the unknown voltages.
By applying KVL, engineers and technicians can analyze circuit behavior and determine voltage sources’ distribution across resistive elements. It helps in identifying voltage drops across individual components to ensure they operate within their specified limits.
KVL is also closely related to the concept of loop analysis, which is a common method for analyzing and solving complex circuits. It enables us to determine circuit currents and voltages using a system of equations based on the summation of voltages around each loop.
Kirchhoff’s Current Law (KCL)
Kirchhoff’s Current Law (KCL) is another fundamental principle in electrical circuit analysis. It states that the total current flowing into a junction or node in a circuit is equal to the total current flowing out of that junction or node. In other words, the algebraic sum of currents at any point in a circuit is zero.
KCL is based on the principle of charge conservation, which states that electric charge cannot be created or destroyed. Therefore, the total current flowing into a junction must be equal to the total current flowing out of it to maintain charge balance.
The application of KCL involves the following steps:
- Identify the nodes in the circuit, which are points where multiple branches connect.
- Assign directions to the currents based on assumptions or known values.
- Apply KCL by summing up the currents at each node, taking into account the directions and polarities.
- Set the sum of the currents equal to zero, considering the signs and directions of the currents.
- Solve the resulting equations simultaneously to find the unknown currents.
By applying KCL, engineers and technicians can analyze current flows and ensure the conservation of current within a circuit. It helps in determining the amount of current each branch carries and ensures that the overall current entering and leaving a node is balanced.
KCL is also closely related to the concept of nodal analysis, which is a method for analyzing and solving complex circuits. Nodal analysis uses KCL equations to determine the node voltages, which can be used to calculate branch currents and analyze circuit behavior.
Overall, Kirchhoff’s Current Law is a crucial tool for circuit analysis and plays a significant role in understanding and designing electrical systems.
Thevenin’s Theorem
Thevenin’s Theorem is a powerful tool in electrical circuit analysis that simplifies complex circuits into an equivalent circuit, allowing for easier analysis and calculation of circuit behavior. It states that any linear electrical network containing voltage sources, current sources, and resistors can be replaced by an equivalent circuit comprising a single voltage source and a single resistor connected in series.
The Thevenin equivalent circuit is characterized by two parameters:
- The Thevenin voltage (Vth): This is the voltage potential between the terminals where the equivalent circuit is connected.
- The Thevenin resistance (Rth): This is the equivalent resistance seen from the terminals of the circuit when all the voltage and current sources are replaced by their internal resistances.
To determine the Thevenin equivalent circuit, the following steps are typically followed:
- Identify the load terminals across which the equivalent circuit is desired.
- Remove the load and find the open-circuit voltage (Voc) across the load terminals. This is the Thevenin voltage (Vth).
- Short-circuit all independent voltage sources and remove all dependent sources in the circuit.
- Calculate the resulting resistance seen from the load terminals. This is the Thevenin resistance (Rth).
- Construct the Thevenin equivalent circuit by connecting the Thevenin voltage source in series with the Thevenin resistance.
Thevenin’s Theorem is particularly useful in simplifying complex circuits, allowing for easier analysis and calculations. It provides a way to represent a circuit with a single voltage source and a single resistor, greatly simplifying subsequent circuit calculations.
Engineers and technicians often use Thevenin’s Theorem to design and analyze circuits because it simplifies the calculations involved in determining circuit responses to different loads. By replacing a complex circuit with its Thevenin equivalent, circuit analysis becomes more straightforward, and the desired voltages and currents can be easily determined.
Overall, Thevenin’s Theorem is an essential concept in electrical engineering, providing a simplified representation of complex circuits, enabling efficient analysis and design.
Norton’s Theorem
Norton’s Theorem is a fundamental concept in electrical circuit analysis that simplifies complex circuits by replacing them with an equivalent circuit consisting of a current source and a parallel resistor. It is a complementary theorem to Thevenin’s Theorem, offering an alternative approach to circuit simplification.
Similar to Thevenin’s Theorem, Norton’s Theorem involves finding an equivalent circuit to study the behavior of a complex electrical network. The Norton equivalent circuit is characterized by two parameters:
- The Norton current (In): This is the current provided by the equivalent circuit and is the same as the short-circuit current through the load terminals.
- The Norton resistance (Rn): This is the equivalent resistance seen from the load terminals when all the voltage and current sources are replaced by their internal resistances.
To determine the Norton equivalent circuit, the following steps are typically followed:
- Identify the load terminals across which the equivalent circuit is desired.
- Remove the load and find the short-circuit current (Isc) flowing through the load terminals. This is the Norton current (In).
- Open-circuit all independent current sources and replace all dependent sources in the circuit with their internal resistances.
- Calculate the resulting resistance seen from the load terminals. This is the Norton resistance (Rn).
- Construct the Norton equivalent circuit by connecting the Norton current source in parallel with the Norton resistance.
With the Norton equivalent circuit, engineers and technicians can simplify complex circuits and analyze circuit behavior more easily. The equivalent circuit can be used to determine current flows, voltage drops, and power dissipation in a circuit without the need for complex calculations.
Norton’s Theorem provides an alternate method to represent complex circuits using a single current source and a parallel resistor. It simplifies circuit analysis by reducing the number of components and simplifying subsequent calculations.
By using Norton’s Theorem, engineers can quickly analyze and design circuits, allowing for efficient troubleshooting, performance prediction, and optimization of electrical systems.
Superposition Theorem
The Superposition Theorem is a valuable tool in electrical circuit analysis that simplifies complex circuits by breaking them down into individual components and analyzing their effects separately. It states that in a linear circuit containing multiple sources, the response at any point can be determined by considering the contribution of each source individually while keeping the other sources turned off.
The key principle behind the Superposition Theorem is that the response of a circuit can be expressed as the sum of the responses produced by each individual source acting alone. This theorem is applicable to circuits consisting of linear components such as resistors, capacitors, and inductors.
To apply the Superposition Theorem, the following steps are typically followed:
- Identify the sources in the circuit, including voltage sources and current sources.
- For each source, keep all other sources turned off, either by replacing voltage sources with short circuits or current sources with open circuits.
- Analyze the circuit by calculating the voltage or current at the desired point using techniques like Kirchhoff’s Laws or Ohm’s Law.
- Repeat the above steps for each individual source.
- Determine the final response by summing up the individual responses obtained from each source.
The Superposition Theorem is particularly useful when dealing with circuits containing multiple sources, allowing engineers and technicians to analyze complex circuits in a step-by-step manner. It simplifies circuit analysis and reduces the complexity associated with solving simultaneous equations.
By applying the Superposition Theorem, engineers can gain a better understanding of how each source contributes to the overall circuit behavior. This information can be used to optimize circuit performance, determine voltage and current distributions, and troubleshoot any issues that may arise.
Overall, the Superposition Theorem provides a powerful technique for analyzing and simplifying complex circuits, making circuit analysis more manageable and efficient.
Mesh Analysis
Mesh Analysis, also known as Mesh Current Analysis or Loop Analysis, is a method for analyzing electrical circuits with multiple current sources and resistors. It simplifies complex circuits by dividing them into individual loops or meshes and applying Kirchhoff’s Voltage Law (KVL) to analyze the voltage drops within each mesh.
The key principle behind Mesh Analysis is to assign loop currents to each mesh and write KVL equations for each loop. This method allows engineers and technicians to determine the currents flowing through each loop and consequently calculate the voltages and power dissipation within the circuit.
The step-by-step process for performing Mesh Analysis is as follows:
- Identify all the loops or meshes in the circuit. A loop is any closed path within the circuit that does not contain any other closed paths.
- Assign a unique current variable to each loop, indicating the assumed direction of the current flow.
- Write KVL equations for each loop by summing up the voltage drops around the loop, taking into account the polarities of the voltage sources.
- Solve the resulting simultaneous equations to find the values of the loop currents.
- Calculate the desired voltages and currents within the circuit using Ohm’s Law or other relevant equations.
Mesh Analysis is particularly useful when dealing with circuits with multiple current sources and resistors. It simplifies the process of solving complex circuits by breaking them down into smaller, more manageable loops. Mesh currents provide a systematic approach to track current flows and determine voltage drops.
By applying Mesh Analysis, engineers and technicians can determine the current flows within each loop, which can help in optimizing circuit performance, identifying potential issues, and designing circuit components more effectively.
Overall, Mesh Analysis is a powerful technique for analyzing complex electrical circuits, allowing for a systematic and efficient approach to determine current flows, voltage drops, and power dissipation within the circuit.
Node Analysis
Node Analysis, also known as Nodal Analysis or Voltage Node Analysis, is a method for analyzing electrical circuits that simplifies complex circuits by using Kirchhoff’s Current Law (KCL) to analyze the currents flowing into and out of each node. It allows engineers and technicians to determine the voltages at different nodes within the circuit.
The key principle behind Node Analysis is to assign voltage variables to each node in the circuit and write KCL equations for each node. This method allows us to determine the currents flowing through each branch and subsequently calculate the voltages at the nodes.
The step-by-step process for performing Node Analysis is as follows:
- Identify all the nodes in the circuit. A node is a point in the circuit where multiple components or branches connect.
- Assign a unique voltage variable to each node, indicating the voltage with respect to a reference node (usually ground).
- Write KCL equations for each node by summing up the currents flowing into and out of the node, taking into account the polarities of the current sources.
- Solve the resulting simultaneous equations to find the values of the node voltages.
- Calculate the desired currents and voltages within the circuit using Ohm’s Law or other relevant equations.
Node Analysis is particularly useful when dealing with circuits with multiple voltage sources and resistors. It simplifies the process of solving complex circuits by breaking them down into smaller, more manageable nodes. Node voltages provide a systematic approach to track voltage differences and determine currents flowing through the branches.
By applying Node Analysis, engineers and technicians can determine the voltage differences at each node, which can help in optimizing circuit performance, identifying potential issues, and designing circuit components more effectively.
Overall, Node Analysis is a powerful technique for analyzing complex electrical circuits, allowing for a systematic and efficient approach to determine voltage differences, current flows, and power dissipation within the circuit.
Capacitor Laws
Capacitors are essential components in electrical circuits, storing and releasing electrical energy. Understanding the fundamental laws governing capacitors is crucial in circuit analysis and design. Here, we will explore the key laws and principles related to capacitors.
Charge-Voltage Relationship:
The charge stored in a capacitor is directly proportional to the voltage across it. This relationship can be expressed by the equation:
Q = C × V
Where Q represents the charge on the capacitor in coulombs, C is the capacitance in farads, and V is the voltage across the capacitor in volts.
Capacitor Energy:
The energy stored in a capacitor can be calculated using the equation:
W = ½ C × V^2
Where W is the energy stored in joules, C is the capacitance in farads, and V is the voltage across the capacitor in volts.
Series Capacitors:
When capacitors are connected in series, the total capacitance (Cs) can be calculated using the reciprocal of the sum of the reciprocals of the individual capacitances:
1/Cs = 1/C1 + 1/C2 + 1/C3 + …
Parallel Capacitors:
When capacitors are connected in parallel, the total capacitance (Cp) is the sum of the individual capacitances:
Cp = C1 + C2 + C3 + …
Equivalent Series Capacitance:
For a combination of series and parallel capacitors, the equivalent series capacitance can be calculated by first determining the total capacitance for capacitors in parallel and then calculating the equivalent capacitance for capacitors in series.
Capacitors also follow specific laws when charging or discharging. When a capacitor charges, the voltage across it increases exponentially until it reaches the source voltage. When a capacitor discharges, the voltage decreases exponentially until it reaches zero.
Understanding the laws and characteristics of capacitors allows engineers and technicians to design and analyze circuits effectively, ensuring optimal performance and reliability. Capacitors play a vital role in various electronic applications, including power supply filtering, timing circuits, signal coupling, and energy storage.
Inductor Laws
Inductors are key components in electrical circuits that store and release magnetic energy. Understanding the fundamental laws governing inductors is crucial in circuit analysis and design. Here, we will explore the key laws and principles related to inductors.
Inductance:
Inductance is the property of an inductor that describes its ability to store magnetic energy. It is denoted by the symbol L and measured in henries (H). The inductance of an inductor depends on its physical characteristics, such as the number of turns in the coil and the core material.
Faraday’s Law of Electromagnetic Induction:
Faraday’s Law states that a changing magnetic field through a loop of wire induces an electromotive force (EMF) or voltage in the loop. This induced voltage is proportional to the rate of change of magnetic flux through the loop and is given by the equation:
E = – dΦ/dt
Where E is the induced voltage, dΦ is the change in magnetic flux, and dt is the change in time.
Inductor Voltage:
According to Faraday’s Law, the voltage across an inductor is directly proportional to the rate of change of current flowing through it. The equation that relates voltage and current in an inductor is:
V = L × di/dt
Where V is the voltage across the inductor, L is the inductance, and di/dt is the rate of change of current.
Inductor Current:
An inductor opposes changes in current flowing through it due to its inertia. In other words, an inductor acts as a “resistor” to changes in current. The equation that describes the relationship between current and voltage in an inductor is:
V = L × (di/dt)
This equation shows that the voltage across an inductor is proportional to the rate of change of current with respect to time, with the inductance being the proportionality constant.
Understanding the laws and characteristics of inductors allows engineers and technicians to design and analyze circuits effectively, ensuring optimal performance and reliability. Inductors play a crucial role in various electronic applications, such as filtering, energy storage, inductive loads, and transformer design.