Why Convert Angles From Degrees to Radians?
Angles play a crucial role in various fields such as mathematics, physics, engineering, and computer science. While there are different ways to measure angles, degrees and radians are the most commonly used units. While degrees are a familiar unit of measurement, radians provide a more precise and convenient way to express angles, especially in complex mathematical functions and calculations.
Converting angles from degrees to radians is essential when working with certain mathematical formulas and trigonometric functions. Radians are the preferred unit of measurement in calculus and advanced mathematics because they allow for more accurate calculations and provide a better representation of the relationship between angles and the functions applied to those angles.
One of the main advantages of radians is that they simplify trigonometric equations and allow for more intuitive calculations. Many mathematical functions, such as sine, cosine, and tangent, are defined in terms of radians, making it necessary to convert angles to radians to use these functions effectively in calculations.
Furthermore, radians offer a more natural representation of angles in circular and trigonometric systems. In radians, an angle of one full revolution (360 degrees) is equal to 2π radians, which simplifies many calculations involving circles, arcs, and angles that exceed 180 degrees.
By converting angles from degrees to radians, you increase your ability to work with complex mathematical functions, trigonometric equations, and scientific calculations. Whether you’re solving differential equations, analyzing waves, or designing intricate geometry, understanding and converting angles to radians will enhance the accuracy, efficiency, and precision of your work.
What Are Degrees and Radians?
Degrees and radians are units used to measure angles. Understanding the difference between these two units is essential when working with various mathematical and scientific calculations.
Degrees are a commonly used unit of measurement for angles. A circle is divided into 360 degrees, with each degree representing 1/360th of a full rotation. Degrees are often used in everyday life, such as measuring angles in geometry or describing temperature changes on a thermometer. For example, a right angle is 90 degrees, and a full revolution around a circle is 360 degrees.
Radians, on the other hand, are a more mathematically oriented unit of measurement for angles. Radians are based on the concept of using the radius of a circle to measure an angle. In a complete circle, there are 2π radians, where π (pi) is a mathematical constant approximately equal to 3.14159. Radians provide a more precise measurement of angles in trigonometry and calculus.
While degrees and radians are different units of measurement, they are directly related. To convert between the two, you can use the conversion factor that one full revolution (360 degrees) is equal to 2π radians. This conversion factor allows you to switch between degrees and radians in various calculations.
It’s important to note that when using trigonometric functions (such as sine, cosine, and tangent) in equations or calculations, many software applications and programming languages often expect angles to be in radians. Therefore, it’s necessary to convert angles from degrees to radians when working with these mathematical functions.
Understanding the differences between degrees and radians and knowing how to convert between them is crucial for accurately representing angles and performing calculations in fields such as mathematics, physics, engineering, and computer science.
The Formula for Converting Degrees to Radians
Converting angles from degrees to radians involves a simple mathematical formula that allows you to switch between the two units of measurement. The formula for converting degrees to radians is:
Radians = (Degrees x π) / 180
In this formula, π (pi) represents the mathematical constant approximately equal to 3.14159. The value of π is used to convert the angle from degrees to the equivalent angle in radians.
To convert a specific angle from degrees to radians, you can substitute the value of the angle into the formula. For example, let’s say you want to convert an angle of 45 degrees to radians. Applying the formula, we have:
Radians = (45 x π) / 180
Simplifying the equation, we get:
Radians = (45 / 180) x π
Radians = (1/4) x π
Therefore, an angle of 45 degrees is equivalent to π/4 radians.
This formula allows you to convert any angle measured in degrees to the corresponding angle in radians. Keep in mind that radians provide a more precise and convenient unit of measurement, especially when working with advanced mathematical calculations and trigonometric functions.
Using the conversion formula, you can seamlessly switch between degrees and radians, allowing you to accurately represent angles and perform complex mathematical operations with ease.
Converting a Single Angle from Degrees to Radians
To convert a single angle from degrees to radians, you can use the formula we discussed earlier: Radians = (Degrees x π) / 180. Let’s walk through the steps to convert a specific angle.
Suppose we want to convert an angle of 60 degrees to radians.
Step 1: Use the formula Radians = (Degrees x π) / 180.
Step 2: Substitute the value of the angle into the formula.
Radians = (60 x π) / 180
Step 3: Simplify the equation.
Radians = π/3
Therefore, an angle of 60 degrees is equivalent to π/3 radians.
It’s important to remember that π is a constant in mathematics and approximately equal to 3.14159. To achieve precise results, it’s best to use the exact value of π rather than an approximation.
Converting a single angle from degrees to radians can be done using this simple formula. By performing the calculation, you can obtain the equivalent angle in radians. This conversion is particularly useful when working with mathematical equations, trigonometric functions, or any scenario where radians are the preferred unit of measurement.
Understanding how to convert angles from degrees to radians allows you to accurately represent angles and perform mathematical calculations more efficiently.
Converting a Range of Angles from Degrees to Radians
Converting a range of angles from degrees to radians is a common task when working with data sets or performing calculations involving multiple angles. To convert a range of angles, you can apply the same conversion formula that we discussed earlier: Radians = (Degrees x π) / 180.
Let’s say you have a set of angles expressed in degrees and you want to convert them all to radians. Here’s how you can do it:
Step 1: Start by listing all the angles you want to convert.
Step 2: Apply the conversion formula to each angle individually.
For example, let’s convert the following angles from degrees to radians: 30°, 45°, and 60°.
Using the formula Radians = (Degrees x π) / 180:
For 30°: Radians = (30 x π) / 180 = π/6
For 45°: Radians = (45 x π) / 180 = π/4
For 60°: Radians = (60 x π) / 180 = π/3
Therefore, the corresponding angles in radians are: π/6, π/4, and π/3.
By applying the conversion formula to each angle in the range, you can convert a set of angles from degrees to radians. This process enables you to work with angles in the preferred unit of measurement for advanced mathematical calculations, trigonometric functions, or any scenario where radians are required.
Converting a range of angles allows you to maintain consistency in your calculations and ensures accurate representation of angles in mathematical and scientific contexts.
Using the RADIANS Function to Convert Angles in Excel
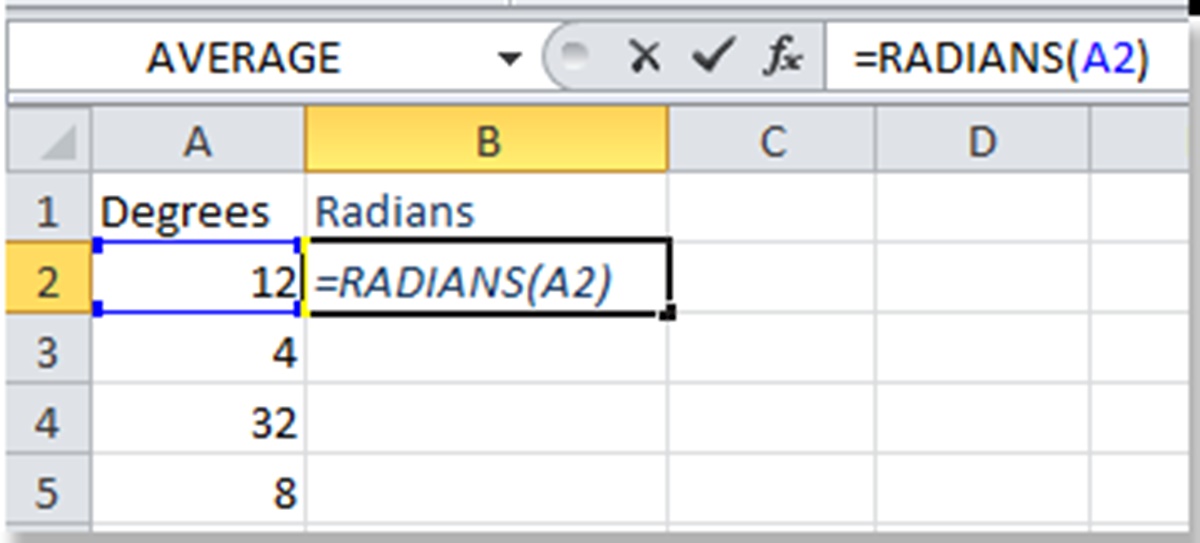
Excel provides a built-in function called RADIANS that makes it easy to convert angles from degrees to radians. The RADIANS function takes an angle in degrees as its input and returns the equivalent angle in radians.
To use the RADIANS function in Excel, follow these steps:
Step 1: Open Excel and enter the degrees you want to convert into a cell. For example, let’s say you want to convert 45 degrees to radians, and you have entered that value in cell A1.
Step 2: In another cell, enter the RADIANS function, followed by the cell reference containing the angle in degrees. In our example, you would enter “=RADIANS(A1)” in cell B1.
Step 3: Press Enter to calculate the equivalent angle in radians.
Excel will return the converted angle in radians based on the value you entered in the RADIANS function. In our example, the cell B1 will display the value π/4, which is the equivalent of 45 degrees in radians.
The RADIANS function in Excel provides a quick and straightforward way to convert angles from degrees to radians without the need for manual calculations. This feature is especially useful when dealing with large datasets or performing complex calculations involving angles in Excel.
By utilizing the RADIANS function, you can ensure accurate conversions and streamline your work when working with angles in degrees and radians within Excel.
Converting Angles Using the CONVERT Function in Excel
Excel provides another useful function called CONVERT that allows you to convert units of measurement, including angles, from one unit to another. By using the CONVERT function, you can easily convert angles from degrees to radians in Excel.
To convert angles using the CONVERT function in Excel, follow these steps:
Step 1: Open Excel and enter the angle you want to convert into a cell. For example, let’s say you want to convert an angle of 60 degrees to radians, and you have entered that value in cell A1.
Step 2: In another cell, enter the CONVERT function and provide the necessary arguments. The syntax for the CONVERT function is: “=CONVERT(number, from_unit, to_unit)”. In this case, you would enter “=CONVERT(A1, “degree”, “radian”)” in cell B1.
Step 3: Press Enter to calculate the converted angle in radians.
Excel will use the CONVERT function to convert the angle from degrees to radians based on the value you entered in cell A1. In our example, the cell B1 will display the value π/3, which is the equivalent of 60 degrees in radians.
The CONVERT function in Excel is a powerful tool for converting various units of measurement, including angles. By utilizing this function, you can streamline your conversions and ensure accurate results when converting angles from degrees to radians within Excel.
It’s worth noting that the CONVERT function can be used for converting other types of units as well, such as length, time, mass, and more. It offers flexibility and convenience in handling unit conversions within the Excel environment.
Converting Angles Using a Custom Formula in Excel
In addition to using built-in functions like RADIANS and CONVERT, you can also create a custom formula in Excel to convert angles from degrees to radians. This method gives you more flexibility and control over the conversion process.
To create a custom formula for converting angles in Excel, follow these steps:
Step 1: Open Excel and enter the angle you want to convert into a cell. For example, let’s say you want to convert an angle of 75 degrees to radians, and you have entered that value in cell A1.
Step 2: In another cell, create a custom formula using the mathematical formula for converting degrees to radians. The formula is: “=A1 * (PI() / 180)”. In our example, you would enter “=A1 * (PI() / 180)” in cell B1.
Step 3: Press Enter to calculate the converted angle in radians.
Excel will apply the custom formula and perform the calculation to convert the angle from degrees to radians based on the value you entered in cell A1. In our example, the cell B1 will display the value approximately equal to 1.30899, which is the equivalent of 75 degrees in radians.
Creating a custom formula allows you to have more control over the conversion process and customize it according to your specific requirements. You can modify the formula to include additional calculations or tailor it to fit different conversion scenarios.
Using a custom formula in Excel for converting angles from degrees to radians provides flexibility and empowers you to easily perform the desired conversion with precision within the Excel environment.
Tips and Tricks for Converting Angles from Degrees to Radians in Excel
Converting angles from degrees to radians in Excel can be a common task, especially when working with trigonometric functions and advanced mathematical calculations. To streamline your conversions and ensure accuracy, here are some helpful tips and tricks:
1. Use built-in functions: Excel provides built-in functions like RADIANS and CONVERT, which simplify the conversion process. These functions are designed specifically for converting angles and offer a straightforward way to obtain the equivalent angle in radians.
2. Utilize the π constant: The mathematical constant π (pi) is crucial in converting angles from degrees to radians. Instead of approximating π, use the PI() function in Excel to get the precise value. This ensures accurate conversions and maintains the integrity of your calculations.
3. Take advantage of cell references: When converting a range of angles, use cell references in your formulas instead of entering each angle individually. This allows you to easily update and modify angles without modifying the formulas manually.
4. Format cells for radians: To ensure clarity and consistency in your data, consider formatting the cells that display radians as the result of your conversions. Applying a custom number format or using the “RADIANS” label in the cell format can help identify the unit of measurement and avoid confusion.
5. Incorporate error handling: If you’re performing calculations with angles, it’s a good practice to handle potential errors that may arise. For example, you can use the IFERROR function to display a specific message or value if an error occurs, ensuring your calculations run smoothly.
6. Document your process: When working with complex calculations, consider adding comments or creating a separate worksheet to document your conversion process. This helps others understand your methodology and allows for easier troubleshooting or modifications in the future.
7. Double-check results: After performing conversions, it’s always good practice to double-check the results, especially when dealing with critical data or precise calculations. Verify your converted angles to ensure they align with your expectations and match the intended units of measurement.
By following these tips and tricks, you can enhance your efficiency, accuracy, and confidence when converting angles from degrees to radians in Excel. Understanding the tools and techniques available in Excel empowers you to leverage the software’s capabilities and effectively manage angle conversions in your calculations and analysis.